# 이상기체 상태방정식이란?
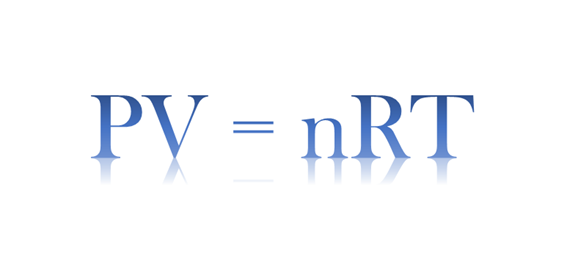
이상기체 상태방정식: 이상기체의 압력, 부피, 질량, 온도 간의 관계를 나타내는 방정식
$P$: 압력
$V$: 부피
$n$: 질량(or 몰 수)
$R$: 기체상수
$T$: 온도
이상기체 상태방정식은 기체에 적용되는 다음 3가지 법칙을 일반화한 것이다.
1) 보일의 법칙: $(P_1V_1 = P_2V_2)$ 압력과 부피는 반비례한다.($P \propto \frac{1}{V}$)
2) 샤를의 법칙: $(\frac{V_1}{T_1}=\frac{V_2}{T_2})$ 부피와 온도는 비례한다. ($V \propto T$)
3) 아보가드로의 법칙: 서로다른 기체 A,B가 있을 때 기체 A,B 의 온도, 부피, 압력이 동일하다면 각 기체의 몰 수는 같다.
이 세가지 법칙을 종합하여 만든것이 바로 이상기체 상태방정식이다.
# 이상기체 상태방정식이 사용 될 수 있는 조건
이상기체 상태방정식은 '이상기체(Ideal Gas)'에만 적용될 수 있는 방정식이므로, 이상기체라는 조건이 필요하다.
이상기체 조건 6가지
1. 이상기체란? Ideal Gas or Perfect Gas $PV=nRT$ 라는 이상기체 상태방정식을 만족하는 기체 $P$: 압력 $V$: 부피 $n$: 기체의 몰수 $R$: 기체상수 $T$: 온도 2. 이상기체 조건 6가지 위에서 언급한 $PV=nRT$..
ikkujun.com
# 실제기체를 이상기체 상태방정식으로 계산해도 될까?
실제 기체는 근사적으로 이상기체 상태방정식에 적용될 수 있습니다. 하지만 세부적으로는 맞지 않기 때문에 정확한 이상기체 상태방정식을 이용하여 실제기체의 정확한 값을 얻을 수는 없습니다.
하지만 실제기체의 압력이 매우 낮고, 온도가 매우 높은 조건이라면 실제기체를 이상기체와 거의 같다고 생각해도 됩니다.
압력이 매우 낮다 -> 분자 자신의 부피를 무시할 정도가 된다.
온도가 매우 높다 -> 높은 온도로 인해 기체 분자간의 상호작용이 거의 무시된다.
그러므로, 압력이 매우 낮고, 온도가 매우 높은 실제기체를 이상기체 상태방정식에 적용하여 꽤 정확한 값을 얻을 수 있습니다.
# 이상기체 상태방정식 계산 예시
다음과 같은 이상기체가 있다고 가정해 봅시다.
$P$: $10atm$
$V$: $5m^3$
$T$: $25$℃
문제 - 이상기체의 몰수(n)를 구하시오
$PV = nRT$ -> $n=\frac{PV}{RT}$ 위 조건대로 대입하면
$n=\frac{10atm\cdot 5m^3}{0.082atm\cdot L/mol\cdot K (25+273.15)K}$ = $2,045mol$ = $2.045kmol$
'자격증' 카테고리의 다른 글
| 2021년 2회 소방설비기사(기계) 기출문제 해설 - 41번,42번,43번,44번,45번 (0) | 2021.08.31 |
|---|---|
| 2021년 2회 가스기사 기출문제 해설 - 36번,37번,38번,39번,40번 (0) | 2021.08.30 |
| 2021년 2회 가스기사 기출문제 해설 - 31번,32번,33번,34번,35번 (0) | 2021.08.28 |
| 2021년 2회 소방설비기사(기계) 기출문제 해설 - 36번,37번,38번,39번,40번 (0) | 2021.08.27 |
| 체적탄성계수(Bulk modulus) (0) | 2021.08.26 |



댓글