내일 드디어 결전의 날인, 소방설비기사(기계) 실기 시험날이다.
(시험 전날 공부해야지 않나..)
작년에 탈락의 고배를 마시고, 보다 열심히 준비했다. 당시 기출문제를 풀어보니 왜 탈락했는지 충분히 알 수 있었다. 제대로 공부하지도 않고 합격하길 바라는 놀부심보였다.
본인과 같이 내일 시험에 도움이 되도록 암기법 하나를 정리해보았다.
우선 본격적인 포스팅 전에 소방호스 그림 하나를 보고 넘어가도록 하자.

소방호스를 간략화한 그림이다. 소방호스로 공급된 물이 소방노즐을 통해 대기중으로 방출되면서 물이 방수된다. 이 물로 소화작업을 하게 된다. 여기서 중요하게 봐야할 점은 노즐의 직경이 끝으로 갈수록 줄어든다는 것이다.
소방호스의 끝부분과 노즐의 끝부분 유량이 동일하므로, 직경이 달라졌으니 유속이 달라져야한다. 즉 노즐의 끝에서 유속이 훨씬 빨라진다.
$Q = \frac{\pi }{4}D^2u$ 식에 의해서 알 수 있다. (D: 직경, u: 유속, Q: 유량)
노즐에 의해 유속이 빨라져, 물이 보다 멀리 방수될 수 있는 것이다. 호스와 노즐의 유속차이 때문에 소방호스가 뱀처럼 움직이는 듯한 모습을 보았을 것이다.

위 사진을 보면 소방관들이 물이 방사되는 힘 때문에 소방호스를 힘겹게 잡는 모습을 볼 수 있다. 바로 이러한 현상이 호스와 노즐에서의 유속차이로 발생하는 것이다. 즉, 유속차이로 인한 반발력이 생기는 것이다.
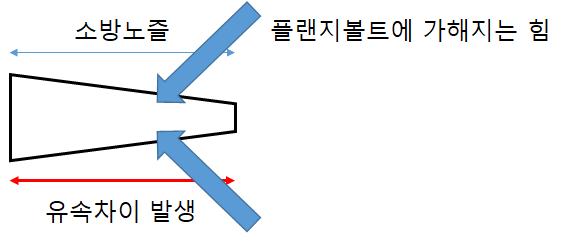
이러한 힘은 소방호스의 플랜지볼트에도 작용하게 되는데, 이를 공식으로 쓰면 다음과 같다. (위에서 말한 반발력과는 다른 힘이다.)
플랜지 볼트에 작용하는 힘
$F = \frac{\gamma A_1Q^2}{2g}(\frac{A_1-A_2}{A_1A_2})^2$
$\gamma $: 물의 비중량
$A_1$: 소방호스의 단면적
$A_2$: 소방노즐의 단면적
$Q$: 유량
딱 봤을 때 거부감이 드는 공식이다. 필자만의 방법으로 좀 간소화해보았다. 그 과정을 같이 알아보자.
먼저 밀도×중력가속도(g) = 비중량이므로
비중량 ÷ 중력가속도 = 밀도를 적용해서 비중량과 중력가속도를 합쳐준다.
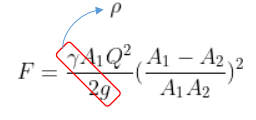
그러면 다음과 같이 바뀐다.
$F = \frac{\rho A_1Q^2}{2}(\frac{A_1-A_2}{A_1A_2})^2$
여기서 유량도 바꿔주어 보자. $Q=A_1u_1 = A_2u_2$ ($A_1$: 소방호스의 단면적, $A_2$: 소방노즐의 단면적)
여기서 $Q = A_1u_1$을 대입해보자.

그리고 우측 $(\frac{A_1-A_2}{A_1A_2})^2$ 괄호 안을 살짝 변형해보면 아래와 같이 바뀌고

$A_1$을 우측 괄호안으로 넣어준다.

그러면

이렇게 바뀐다. 여기서 $A_1 = \frac{\pi }{4}D_1^2$, $A_2 = \frac{\pi }{4}D_2^2$ 을 괄호 한 $A_1, A_2$에 각각 대입하면
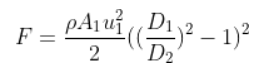
원래 공식에 비하면 훨씬 간단해졌다. 괄호한을 외우는 방법은 직경이 큰 $D_1$이 위로 온다고 생각하면 된다.
이렇게 어떤 공부를 하든 본인만의 방법으로 정리를 하거나 간단 및 간소화시키는 과정은 공부를 하는 데 매우 도움이 된다.
<참고사항>
운동량 차이로 인한 반발력과 플랜지 볼트에 작용하는 힘은 다르다.
$F = \rho Q(u_2-u_1)$
소방호스와 소방노즐의 유속차이 × 유량 × 물의 밀도를 계산하면 된다.
'자격증' 카테고리의 다른 글
| 벤츄리 효과(Venturi Effect) - 포소화약제 혼합장치 (0) | 2021.07.19 |
|---|---|
| 베르누이 방정식 - 유체의 에너지 보존법칙 (0) | 2021.07.18 |
| 무차원수 정리 (0) | 2021.07.08 |
| 할론 소화약제, 할로겐화합물 소화약제 차이점 (0) | 2021.06.29 |
| 위험물산업기사 2020년 1,2회 통합 21,22,23,24,25번 풀이 (0) | 2021.06.25 |


댓글