728x90
반응형
728x170
무차원수
Dimensionless Number
측정 단위에 독립적인 값을 갖는 수
일반적인 물리량(시간, 길이, 질량 등)은 단위를 갖는다. 하지만 무차원수는 단위가 없다. 그래서 어떤 현상 등을 설명할 때 매우 유용하게 쓰인다. 각 무차원수의 이름은 해당 무차원수를 발견한 학자의 이름을 붙여서 부른다.
물이나 공기 등의 유체에 관한 공학적 계산에 주로 사용된다.
공학적 계산에 어떻게 사용되는지 간단한 예시를 통해 알아보자.
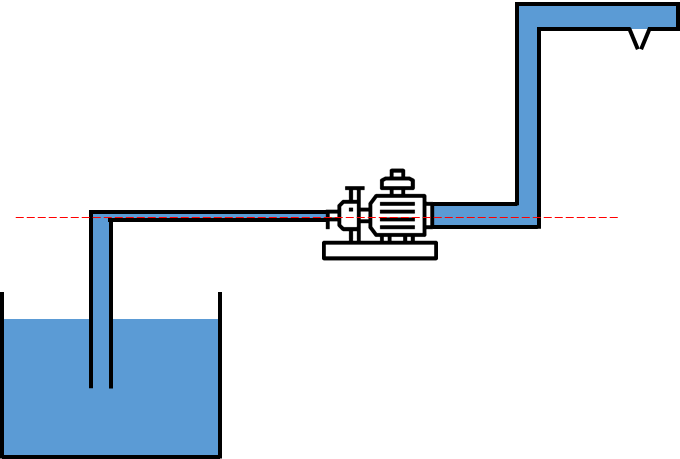
위 그림과 같이, 탱크에 저장된 물을 건물 상층의 스프링클러까지 보낼 수 있도록 펌프와 배관을 설계하려고 한다. 배관을 지나는 물이 층류인지 난류인지에 따라 배관의 두께가 달라진다. 배관의 두께가 두꺼워지면 그만큼 비용이 더 많이 필요하다. 이때, $Re$(Reynolds Number)라는 무차원수를 이용해 유체가 층류인지 난류인지를 판단하고 유체의 흐름에 맞는 배관두께를 계산해서 보다 합리적인 설계가 가능하다.
무차원수 정리표
| 번호 | 무차원수 이름 | 기호 | 정의 | 특징 | 비고 |
| 1 | 레이놀즈 수 Reynolds Number |
$Re$ | $Re = \frac{D\rho u}{\mu }$ 관성력/점성력 $D$ : 관 직경 $\rho$: 유체 밀도 $u$: 유체 유속 $\mu$: 유체 점도 |
관 속을 흐르는 유체가 층류인지 난류인지 판단할 때 사용한다. $Re$ <2100 층류 $Re$ >4000 난류 |
|
| 2 | 프란틀 수 Prandtl Number |
$Pr$ | $Pr=\frac{C_{p}\mu }{k}$ 운동량계수/열전달계수 $C_{p}$: 유체 열용량 $\mu$: 유체 점도 $k$: 유체 열전도도 |
평판을 따라 흐르는 유체에서, 속도경계층과 온도경계층이 어떻게 확산되는지 나타내는 무차원수 | |
| 3 | 너셀 수 Nusselt Number |
$Nu$ | $Nu = \frac{hL}{k}$ 대류열전달/전도열전달 $h$: 대류열전달계수 $L$: 특성길이 $k$: 유체의 열 전도도 |
열이 전달되는 상황에서, 대류에 의한 열전달의 크기와 전도에 의한 열전달의 크기 비율 $Nu =1$ 라는 건, 대류와 전도에 의한 열전달 크기가 같다는 뜻이다. |
|
| 4 | 웨버 수 Webber Number |
$We$ | $We = \frac{\rho u^2L_{c}}{\sigma }$ 관성력/표면장력 $\rho$: 유체 밀도 $u$: 유속 $L_c$: 특성길이(대체로 액체방울의 직경) $\sigma$: 표면장력[$N/m$] |
유체가 흩뿌려지는 상황, 분출되는 상황에서 유체가 어떤 모양이 될지를 예측해볼 수 있는 무차원수. 웨버수가 작을수록 구형의 모양을 잘 유지하게 된다. |
|
| 5 | 푸리에 수 Fourier Number |
$Fo$ | $Fo = \frac{kt}{c_p\cdot \rho \cdot L^2}=\frac{\alpha t}{L^2}$ 열전도/열저장 $k$: 열전도계수 $\alpha$: 열확산계수 $t$: 시간 $c_p$: 열용량 $L$: 특성길이 $\rho$: 밀도 |
물체 내부의 열전달 속도 | |
| 6 | 프루드 수 Froude Number |
$Fr$ | $Fr=\frac{V}{gL}$ 관성력/중력 $V$: 유속 $g$: 중력가속도 $L$: 특성길이 |
중력의 영향에 따른 유동형태를 판별할때 사용 | |
| 7 | 마하수 Mach Number |
$Ma$ | $Ma = \frac{u}{c}$ 유속/음속 $u$: 유속 $c$: 음속 |
압축성 유체에서 주로 사용되는 무차원수. 마하수에 따라 유체의 특성이 달라지게 된다. |
|
| 8 | 오일러 수 Euler Number |
$Eu$ | $Eu = \frac{\Delta P}{\rho u^2}$ 압력/관성력 $\Delta P$: 압력차 $\rho$: 유체 밀도 $u$: 유속 |
오리피스를 통과하는 유동, 공동현상(cavitation) 판단, 유체에 의해 생성되는 항력과 양력 효과 판단 |
728x90
반응형
그리드형
'자격증' 카테고리의 다른 글
| 베르누이 방정식 - 유체의 에너지 보존법칙 (0) | 2021.07.18 |
|---|---|
| 소방설비(기계) - 플랜지 볼트에 작용하는 힘 공식 암기법 (0) | 2021.07.09 |
| 할론 소화약제, 할로겐화합물 소화약제 차이점 (0) | 2021.06.29 |
| 위험물산업기사 2020년 1,2회 통합 21,22,23,24,25번 풀이 (0) | 2021.06.25 |
| 위험물산업기사 2020년 1,2회 통합 16,17,18,19,20번 풀이 (0) | 2021.06.24 |



댓글